pymc3をいじってみようの会 vol.2-サンプルデータを生成する練習1(指数分布)-
前回までのあらすじ
この本を主に勉強の指針にしています。

Pythonで体験するベイズ推論 PyMCによるMCMC入門
- 作者: キャメロンデビッドソン=ピロン,玉木徹
- 出版社/メーカー: 森北出版
- 発売日: 2017/04/06
- メディア: 単行本(ソフトカバー)
- この商品を含むブログを見る
前回までにやったこと k-mawa.hateblo.jp
前回はインストールをただしてみただけであったので今回もとりあえず前にちょっと進めていく。毎日ちょっとずつでもやるのがよい気がするので・・・
とりあえず今後毎回作った予測モデルがどれだけの精度なのか実サンプルデータセットではなく、もっと簡単にささっと検証用のテストデータを作ったりする必要があるとおもう。と、いうことで、何かの分布にそったデータ・セットをつくる練習である。
今回の勉強素材
pymc3のドキュメントのコードを参考に引用しつつ1個1個検証していきます。 Continuous — PyMC3 3.2 documentation
とりあえずやってみよう
- 1:とりあえず必要なモジュールをインポート。
>>>import matplotlib.pyplot as plt >>>import numpy as np >>>import scipy.stats as st
まあよく見る顔ぶれですかね・・・
- 2:numpyのlinspaceのメソッドで、等差数列のアレイを作っておく。あとで確率分布にぶち込むための数値データの固まりをつくっておきます。
>>>x = np.linspace(0.0, 5.0, 1000) #start0, stop5 , 項数1000 等差数列を生成するメソッド
>>>print("x[:20]===>",x[:20])
>>>print("x.shape===>",x.shape)
x[:20]===> [ 0. 0.00500501 0.01001001 0.01501502 0.02002002 0.02502503
0.03003003 0.03503504 0.04004004 0.04504505 0.05005005 0.05505506
0.06006006 0.06506507 0.07007007 0.07507508 0.08008008 0.08508509
0.09009009 0.0950951 ]
x.shape===> (1000,)
- 3:指数分布を描写する関数をつくる
>>>f = lambda lam : st.expon.pdf(x, scale=1.0/lam) >>>f <function __main__.<lambda>>
ラムダ式(無名関数)とは何かを軽く復讐しておきましょう。 簡単に言うと、def aiueo(hoge) ≒ lambda hoge : 関数の中身(hoge) という感じですね
参考URLです
expon.pdfって何??と思ったので調べます。英語の勉強です。 確率密度関数→probability density function(PDF)と訳することがわかりました。 exponはexponential =指数の意。つまりexpon.pdfは指数分布の確率密度関数という意味になる
参考URLです。わかりやすい
これも分かりやすいコードもついている
- 4:指数分布の確率密度関数に代入した値をプロットする関数をつくる
>>>plot_pdf = lambda lam : ax.plot(x, f(lam), label=r'$\lambda$={0}'.format(lam))
>>>
これはさっき作った等差数列を確率密度関数にぶち込んで描写するための無名関数です
- 5:描写してみる
>>>fig, ax = plt.subplots()
>>>print("====fig===")
>>>print(fig)
>>>print("====ax===")
>>>print(ax)
>>>print("#figはプロットするフィールド全体のようなイメージかな、そのオブジェクト。axは軸についてのオブジェクト")
#λが各0.01,0.2,0.5,1.2,10,100の指数分布
>>>plot_pdf(0.01)
>>>plot_pdf(0.2)
>>>plot_pdf(0.5)
>>>plot_pdf(1.2)
>>>plot_pdf(10)
>>>plot_pdf(100)
>>>plt.legend(loc='upper right', frameon=False)
>>>ax.set(xlim=[0,5], ylim=[0,1.6], xlabel='x', ylabel='f(x)')
>>>plt.show()
====fig===
Figure(432x288)
====ax===
Axes(0.125,0.125;0.775x0.775)
figはプロットするフィールド全体のようなイメージかな、そのオブジェクト。axは軸についてのオブジェクト
描写された結果
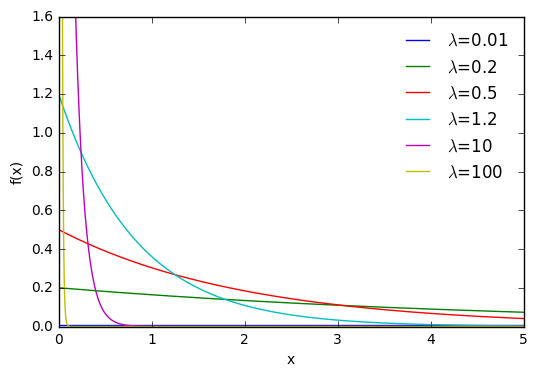
とりあえず描写ができました。引数に入れ込んだ値と各返り値のセットをアレイに入れたいんだがそれはまた今度やっていこう
Jupter Noterbookでのコ−ド履歴
続く(予定)